شما به عنوان دانشجوی کارشناسی در رشته ریاضیات یا یک علاقه مند به یادگیری دروس رشته ریاضی، در ترم های اول باید دو درس اجباری

مهندسی کنترل یک علم بین رشته ای است که می تواند در سایر رشته های مهندسی مانند “مهندسی مکانیک”، “مهندسی برق”، “مهندسی هوافضا”، “مهندسی شیمی”

نظریه اعداد یکی از شاخه های ریاضیات است که به روابط بین اعداد صحیح (اعداد طبیعی مثبت و منفی و صفر) می پردازد که به

مکانیک کلاسیک یا “دینامیک کلاسیک” به طور کلی درباره اعمال قوانین نیوتن در یک سیستم دینامیکی و استخراج معادلات حرکت سیستم است. معمولاً ابتدا دیاگرام

بهترین مثال استفاده از هوش مصنوعی در رباتیک، ربات های انسان نما هستند. ویدئوی زیر نحوه تکامل روبات های انسان نما را از سال ۲۰۰۹

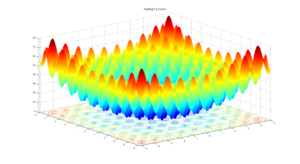
در بسیاری از زمینه های علوم محض و رشته های مهندسی، ما با مسائلی روبرو می شویم که نیازمند اینست که یک تابع ریاضی بهینه

فیزیک کلاسیک، به واسطه کارهای نیوتون در “مکانیک” و معادلات مشهور ماکسول در “الکترومغناطیس” و همچنین قوانین کپلر برای “مکانیک سماوی”، به خوبی شناخته شده